By Dr. Nick Kollerstrom
Greetings — Dr. Nick Kollerstrom here. I’m excited to share with you my exploration of a remarkable crop formation that appeared on 8th June 2025 at Faulkners Circle, just outside Avebury in Wiltshire.
What drew me in initially was some excellent preliminary geometry done by researcher Bert Janssen. His analysis sparked my curiosity, and I decided to dig deeper into what I believe is a stunning example of latent geometric intelligence — the kind we often see in formations that feel “beyond human.” [Link to Bert’s original analysis.]
It Begins with a Circle
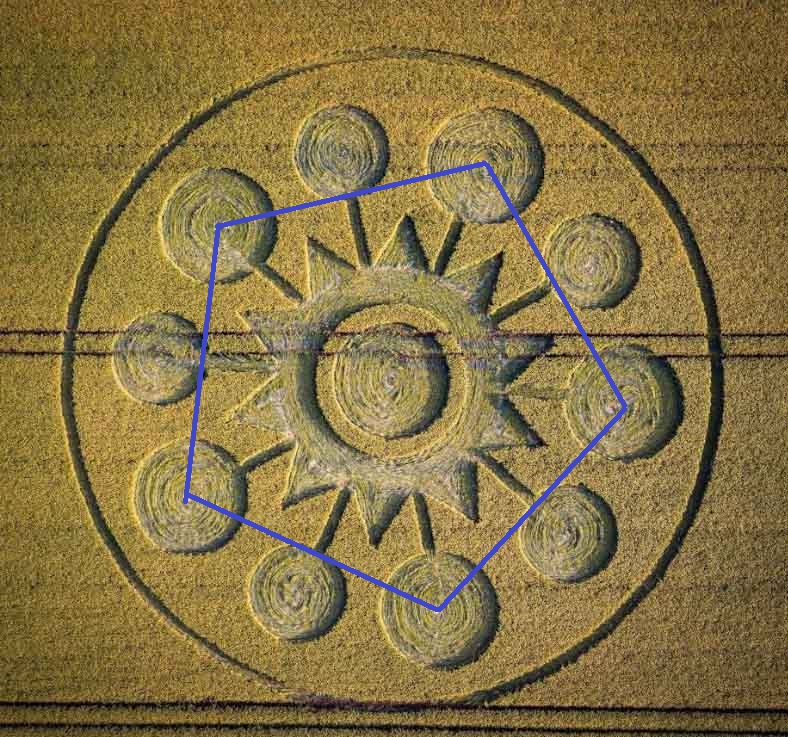
The formation begins simply: ten circles evenly spaced around a large central ring. Bert placed this ring inside a square, with the square’s corners touching the perimeter of the circle — a placement that gives us a fascinating result. The two circles — inner and outer — have radii in the ratio of √2, meaning one has twice the area of the other. A lovely piece of harmonic symmetry right from the start.
He put another circle around the outside of the five ‘bigger’ circles just touching them, and that appeared to be in a ‘squaring the circle’ relation to the square – so they both had the same perimeter. That defined the size of the five bigger circles, and means that they are 27.3% of the size of the large circle that goes thru their centres (trust me!). That is exactly the size of the Moon in relation to the Earth, 27.3%! This calculation assumes that Bert is correct and that a circle-squaring has in fact been used.

The famous circle-squaring construction discovered years ago by John Michell gives likewise this very same Earth-Moon size ratio, and its
rather similar isn’t it?
Next we move to a fivefold design. The Masters of Harmony have fixed the sizes of the five smaller circles such that they just touch a regular pentagon, which links the centres of the five bigger circles. This is a tenfold division of the circle
Moving to the inner part of the design, we notice a ‘latent circle’ which defines its magnitude. A tenfold star at the centre touches this circle, which also touches the five circles we just looked at. Thereby inner and outer part of the design are linked together. This is a hallmark of Circlemaker art, whereby inner and outer aspects of a design are different and yet complement each other, they are subtly linked together.

That star at the centre turns out to have a rather unexpected twenty-fold design. This is a rather beautiful and sublime latent geometry at the centre. By ‘latent’ we mean that it is not at once evident, but was used in the construction. The lines of this stellar pattern frame the circle at the centre and the inner ring of that circle has the same size as the five outer circles we started off with.
You might take the view that the centre of this formation is ‘access denied,’ i.e. no-one could have stood at the centre while making it! By whatever means, a circle was divided at 18° intervals to construct this design.


But wait, it gets better. That pattern at the centre is woven of two separate pentagonal structures, which don’t really meet – here’s one of them:

That is one ingenious pentagon, or is it a decagon? Whatever it is, I suggest that we have never seen such a design before!
In this formation, as in others that have left a lasting impression on me, we see a geometry that is not just clever but meaningful. It’s as if the design is speaking in a language we have only half remembered — the language of harmony, of proportion, of Earth and Moon and cosmos.
I hope this breakdown has helped illuminate some of the quiet genius behind this crop circle. My thanks again to Bert Janssen for the spark that led me into this delightful analysis.
— Dr. Nick Kollerstrom



Nice work and a great find. Thanks!